Extended Euclidean Algorithm (The Pulveriser) - Explanation and Implementation
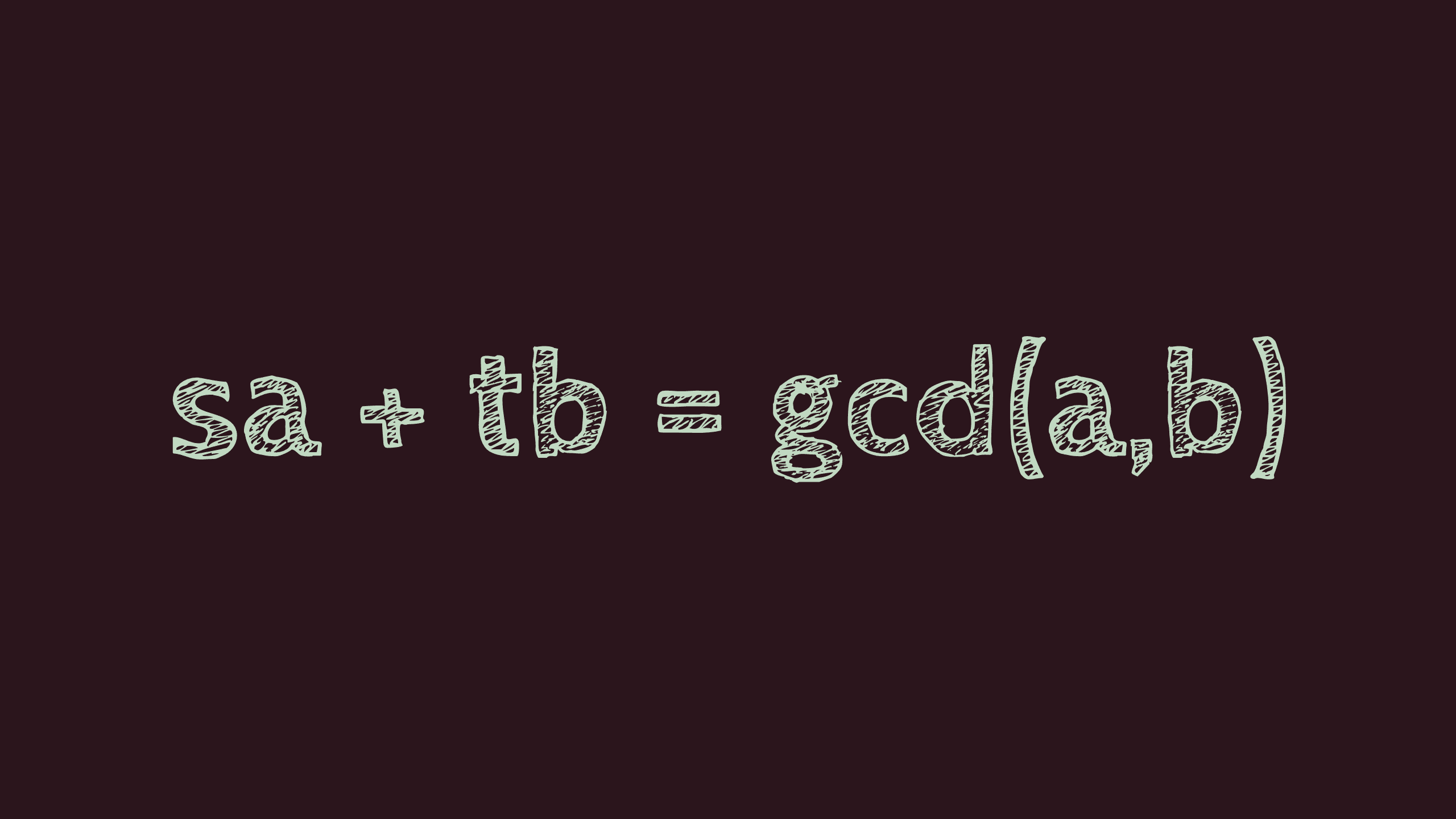
A little Background
The Extended Euclidean Algorithm is, as the name suggests, an extension to the Euclidean algorithm and in addition to gcd, it also computes the coefficients of Bézout's identity. The algorithm has roots dating back to ancient India where it was called Kuṭṭaka, meaning The Pulveriser, considered as the precursor to what is today known as the Extended Euclidean Algorithm.
Applications
One of the most common uses of the Extended Euclidean Algorithm is to solve linear Diophantine equations.
It is also used extensively in the field of cryptography, Extended Euclidean Algorithm forms the basis of computing Modular Multiplicative Inverse, which is a key step required in the famous RSA public key cryptographic algorithm to derive the key pairs.
Bézout's Identity
Bézout's Identity is the following theorem in Number Theory(from Wikipedia).
Let a and b be integers with greatest common divisor d. Then there exist integers x and y such that ax + by = d. More generally, the integers of the form ax + by are exactly the multiples of d.
or informally
gcd of two integers a and b can be expressed as an integer linear combination of a and b.
The Algorithm
Euclid's Algorithm
According to Euclid's algorithm
gcd(a,b) = gcd(b, a%b)
this essentially means that gcd of a and b is the same as gcd of b and the remainder of a/b, if we compute this recursively until b becomes 0(this also happens to be the base case) then we are left with a, and this new value of a is the gcd of the two original numbers a and b.
Here are the high-level steps of Euclid's Algorithm
Step 1(base case): if
bis 0, thenais the gcdStep 2: else set
a = previous band setb = a mod b.Step 3: Repeat Step 2 until we arrive at the base case.
Here's a Java implementation of Euclid's Algorithm.
public int gcd(int a, int b){
if(b==0)
return a;
return gcd(b,a%b);
}Extended Algorithm
One of the key concepts that we'll be using is the basic Division Algorithm i.e
For any given two positive integers x and y, there exist two integers q and r which satisfy the equation
x = qy + r where 0 <= r <= y
x -> Dividend, y -> Divisor
q -> Quotient, r -> remainder
If you think about the previously shown Euclid's Algorithm again, you'll realize that gcd is actually the last non-zero remainder from all of the performed steps.
And, from the Division Algorithm we just saw, we have a way to represent the remainder in terms of a linear combination of the quotient, dividend, and divisor, all we need to do is rearrange the equation the way we want it.
x = qy + rcan also be written asr = x - qy
As part of the Extended Euclidean Algorithm, we just need to maintain some extra information at every step of the basic Euclid's Algorithm.
So, we now have the following important observations/tools that will help us compute Bézout's coefficients.
1. gcd(a,b) = gcd(b, a mod b)
2. gcd(a,b) is the last non-zero remainder.
3. r = x - qy
Now, all we need to do is represent the remainder r as an integer linear combination of a and b at every step of Euclid's algorithm and keep track of the coefficients and keep on updating them, once we are at the final step of the algorithm, we will have the last non-zero remainder expressed as the linear combination, which is also the gcd and that is exactly what we need.
It will be easier to understand with an example.
Example
Let's take two integers a=785646, b=252
Step 1)
785646 = (3117 * 252) + 162
// can also be written as
162 = 785646 - (3117 * 252)
//replace values with a and b
162 = 1*a - 3117*bStep 2) We now have a=252, b=162
252 = (1 * 162) + 90
// or
90 = 252 - (1 * 162)
// from previous step we know that
b=252
162 = 1*a -3117*b
//after substituting these values we get
90 = b - (a - 3117b)
90 = -a + 3118bStep 3) a=162, b=90
162 = 90 + 72
// or
72 = 162 - 90
// from previous steps
162 = 1*a -3117*b
90 = -a + 3118b
// substitue values
72 = (a - 3117b) - (-a + 3118b)
72 = 2a - 6235bAfter repeating the steps few more times you'll finally end up with the following result.
| Step | a | b | r | r as a linear combination |
|---|---|---|---|---|
| 1. | 785646 | 252 | 162 | a - 3117b |
| 2. | 252 | 162 | 90 | -a + 3118b |
| 3. | 162 | 90 | 72 | 2a - 6235b |
| 4. | 90 | 72 | 18 | -3a + 9353b |
| 5. | 72 | 18 | 0 |
At Step 5 we get the remainder as 0, this means the gcd of a and b is 18 and from Step 4 we have 18 expressed as the linear combination of a and b.
So here we have it, gcd expressed as the linear combination -3a + 9353b
Bézout's coefficients:
s= -3
t = 9353
gcd(785646,252) = (-3 * 785646) + (9353 * 252) = 18
Implementation in Java
public static void extendedEuclidean(long a, long b){
long oldR = a, r=b;
long oldS = 1, s = 0;
long oldT = 0, t = 1;
while(r != 0){
var quotient = oldR / r;
var rTemp = r;
r = oldR - quotient * r; oldR = rTemp;
var sTemp = s;
s = oldS - quotient * s; oldS = sTemp;
var tTemp = t;
t = oldT - quotient * t; oldT = tTemp;
}
System.out.printf("Coefficients: s:%s, t:%s%n", oldS,oldT);
System.out.printf("GCD:%s%n", oldR);
}